马小混

动态规划 - 最长公共子序列(连续)

2019/01/02

动态规划 - 最长公共子序列(连续)

一、题目描述

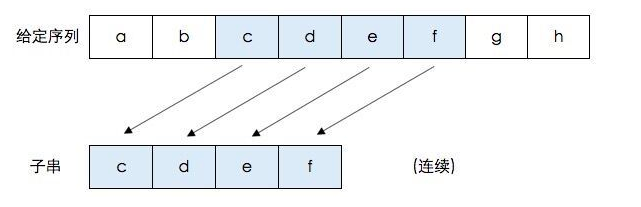
longest_common_sub_ii

二、ruby方案

2.1 思路设计

不能使用暴力搜索方法。一个长度为n的序列拥有 2的n次方个子序列，它的时间复杂度是指数阶，太恐怖了。

动归还是可以使用上题的状态，而且情况更加简单

maxLen(i, j) 表示字符串a以i为结尾子串，字符串b以j为结尾的子串的最大公共子串

if str_a[i] == str_a[b]
      maxLen(i, j) = maxLen(i - 1, j - 1) + 1
else
  maxLen(i, j) = 0

2.2 代码

def longest_common_sub(s1, s2)
  s1_len = s1.size
  s2_len = s2.size

  dp = Array.new(s1_len) { Array.new(s2_len, 0) }
  dp[0][0] = (s1[0] == s2[0] ? 1 : 0)
  dp[0][1] = (s1[0] == s2[1] ? 1 : 0)
  dp[1][0] = (s1[1] == s2[0] ? 1 : 0)

  1.upto(s1_len - 1).each do |i|
    1.upto(s2_len - 1).each do |j|
      if s1[i] == s2[j]
        dp[i][j] = dp[i-1][j-1] + 1
      else
        dp[i][j] = 0
      end
    end
  end

  dp.flatten.max
end


Show Disqus Comments

Post Directory