动态规划 - 最长公共子序列(不连续)

描述

求出这样的一个最长的公共子序列的长度：

子序列中的每个字符都能在两个原串中找到， 而且每个字符的先后顺序和原串中的先后顺序一致。

示例：

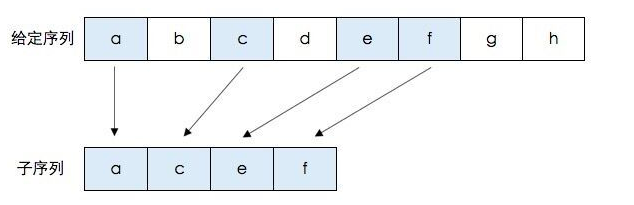
分析：

注意点：

1. 可以不连续
2. 公共长度可以为0

解决动归问题，最重要的就是确定问题的状态。

首先要确定问题的状态，数字三角形的状态 是坐标（i,j）,最长上升子序列的状态是下标 i。

那么这个问题的状态是什么？

maxLen(i,j) i,j分别是两个字符串的下标，maxLen就表示字符串a左边i个字符串 和 字符串b左边j个字符串 的最大公共子序列的长度。

所以 maxLen(i,j) 就是本例题的状态。

推导过程

递推公式：

if(a[i] == b[j]) {
    maxLen(i,j) = maxLen(i-1, j-1) + 1;
} else {
    maxLen(i,j) = Math.max(maxLen(i-1, j), maxLen(i, j-1));
}

代码实现

我的总结

1、状态确定 是 动态规划算法的 第一步。

这是解决问题的第一个思考方向。

2、本题中 maxLen(i,j)是本题的状态。

注意一点，maxLen不要想成是函数，而是一个数组，其实应该是 maxLen[i][j];

3、for循环，无论是人人为我，还是我为人人，都是顺序操作的。

不同的是前者从下标1开始，后者从下标0开始；

4、已经总结了三个动态规划，有一点感觉。

1、没有递归

2、循环

3、状态确定 （状态 和 表达式）