每日算法 - 最长回文子串
题目描述
给定一个字符串 s,找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。
示例 1:
输入: "babad"
输出: "bab"
注意: "aba" 也是一个有效答案。
示例 2:
输入: "cbbd"
输出: "bb"
答题思路
1 动态规划
思路一
设状态dp[j][i]表示索引j到索引i的子串是否是回文串。则转移方程为:
状态转移方程:
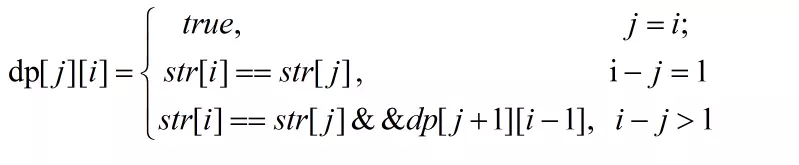
则dp[j][i]为true时表示索引j到索引i形成的子串为回文子串,且子串起点索引为j,长度为i - j + 1。
算法时间复杂度为O(N ^ 2)。
# @param {String} s
# @return {String}
# 回文字符串去掉首尾一定还是回文字符串
# f(i, j) = f(i+1, j-1) + 2 s[i] == s[j]
def longest_palindrome(s)
return "" if s.nil? || s.empty?
len = s.size
return s if len == 1 || s.chars.uniq.size == 1
dp = Array.new(len){Array.new(len, false)}
max_len = 1 # 保存最长回文子串长度
start = 0 # 保存最长回文子串起点
0.upto(len - 1).each do |i|
0.upto(i).each do |j|
if (i - j < 2)
# 从小到大,所以dp[j][i]
dp[j][i] = true if (s[i] == s[j])
else
dp[j][i] = (s[i] == s[j] && dp[j + 1][i - 1])
end
if dp[j][i] && max_len < (i - j + 1)
max_len = i - j + 1
start = j
end
end
end
return s[start...(start + max_len)]
end
思路二
1、两种情况: 单回文 和 双回文 形式;
1、状态: maxLen(n) 下标n为中心点的最长回文字符串长度。
那么:
单回文:
left = right = n;
while(left >= 0 && right < length && arr[left] == arr[right]) {
maxLen(n) += 1;
}
双回文:
left = n;
right = n + 1;
while(left >= 0 && right < length && arr[left] == arr[right]) {
maxLen(n) += 1;
}
2、是否可用动态规划?
1、最优子结构符合。
2、无后效性也符合。
####代码实现
1、先按照以上状态找到每个下标对应的最长单回文和双回文的长度。
2、枚举最长的即可。
3、具体细节不必考虑, 比如一个字符是不是回文,空怎么算,这些都是细节,不是思想
ruby代码:
# @param {String} s
# @return {String}
def longest_palindrome(s)
if s.empty?
return ""
elsif s.length == 1
return s
end
single_length = []
double_length = []
#1 初始化回文长度为0
(0..s.length).each do |index|
single_length[index] = 0
double_length[index] = 0
end
#以每个字符为中间值得最大回文字符串长度(单回文,或者双回文)
(1..s.length - 1).each do |index|
single_index = index
double_index = index
#单回文
(single_index..s.length).each do |index1|
abs = index1 - index
left = index - abs - 1
rigth = index + abs + 1
if s[left].eql?(s[rigth]) && left >= 0 && rigth < s.length
single_length[index] += 1
left -= 1
rigth += 1
else
break
end
end
#双回文
(double_index..s.length).each do |index2|
abs = index2 - index
left = index - abs - 1
right = index + abs
if s[left].eql?(s[right]) && left >= 0 && right < s.length
double_length[left] += 1
left -= 1
right += 1
else
break
end
end
end
single_max = single_length.sort.last
single_index = single_length.index(single_max)
double_max = double_length.sort.last
double_index = double_length.index(double_max)
res = single_max > double_max ? s[single_index - single_max..single_index + single_max] :
s[double_index - double_max + 1, double_index + double_max]
if res.empty?
s[0]
else
res
end
#return [single_max, single_index, double_max, double_index]
end
2 中心扩展法
中心扩展就是把给定的字符串的每一个字母当做中心,向两边扩展,这样来找最长的子回文串。算法复杂度为O(N^2)。
需要考虑两种情况:
- 长度为奇数的回文串,比如a, aba, abcba
- 长度为偶数的回文串,比如aa, abba
#include <iostream>
#include <cstring>
using namespace std;
string longestPalindrome(string &s)
{
const int len = s.size();
int maxlen = 1;
int start = 0;
for(int i = 0; i < len; i++)//求长度为奇数的回文串
{
int j = i - 1, k = i + 1;
while(j >= 0 && k < len && s.at(j) == s.at(k))
{
if(k - j + 1 > maxlen)
{
maxlen = k - j + 1;
start = j;
}
j--;
k++;
}
}
for(int i = 0; i < len; i++)//求长度为偶数的回文串
{
int j = i, k = i + 1;
while(j >= 0 && k < len && s.at(j) == s.at(k))
{
if(k - j + 1 > maxlen)
{
maxlen = k - j + 1;
start = j;
}
j--;
k++;
}
}
return s.substr(start, maxlen);
}
int main()
{
string s;
cout << "Input source string: ";
cin >> s;
cout << "The longest palindrome: " << longestPalindrome(s);
return 0;
}
3 Manacher算法
Manacher算法并没有看,因为感觉不是普适算法,没必要专门学习。

Show Disqus Comments