动态规划 例题二、 最长上升子序列(百练2757)

1、题目描述

一个数的序列bi，当b1 < b2 < … < bS的时候，我们称这个序列是上升的。

对于给定的一个序列(a1, a2, …, aN)，我们可以得到一些上升的子序列(ai1, ai2, …, aiK)，这里1 <= i1 < i2 < … < iK <= N。

比如，对于序列(1, 7, 3, 5, 9, 4, 8)，有它的一些上升子序列，如(1, 7), (3, 4, 8)等等。这些子序列中最长的长度是4，比如子序列(1, 3, 5, 8).

你的任务，就是对于给定的序列，求出最长上升子序列的长度。

输入

输入的第一行是序列的长度N (1 <= N <= 1000)。第二行给出序列中的N个整数，这些整数的取值范围都在0到10000。

输出

最长上升子序列的长度。

样例输入

7

1 7 3 5 9 4 8

样例输出

4

2、题目分析

如何使用动态规划的思路来解决问题呢。

首先自然而然想到的是， f(n) 前n个字符序列的最长子序列。但是存在一个问题，就是这个函数不满足’无后效性’。

有多种情况会构成f(n)的最长子序列，所以f(n+1)的构成不定；也就是说无法由f(n)获取f(n+1).

转换思路：

以第n个字符为结尾的最长序列是f(n), 然后枚举最大值即可。 而f(n)的长度是f(n)之前的字符比第n个字符小的，最长序列 + 1， 即。

for (int i = 1; i < n; i++) { if (a[i] < a[n]) { f(n) = Math.max(f(n), f(i) + 1); } }

不断去更新f(n)的值。

不同的解法

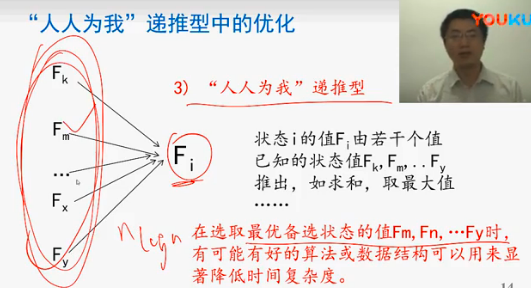
1、人人为我 解法：

人人为我：

以本例为例，人人为我的解法是，f(n)就是"我"，为了求出f(n), 1到n-1的最长子序列都要求出来，这些子问题的解都是为了求f(n).

这就是人人为我。如下图

// 序列
int[] list = new int[]{1,2,3,4,5,1,2,8};
//f（n）序列
int[] val = new int[list.length];

/**
 * 初始化，至少长度为1
 */
for (int i = 0; i < list.length; i++) {
     val[i] = 1;
}

for (int i = 1; i < list.length; i++) {
     for (int j = 0; j < list.length; j++) {
          if (list[j] < list[i]) {
             val[i] = Math.max(val[i], val[j] + 1);
          }
     }
}

2、我为人人 解法：

我为人人：

以本例为例，我为人人的解法是，f(n)就是”我”，求出f(n)之后, 要更新f(n)之后的值，注意是更新而不是最终确定了最大值.这个值不一定是最终值。

for (int i = 0; i < list.length - 1; i++) {
     for (int j = i + 1; j < list.length; j++) {
         if (list[i] < list[j]) {
            val[j] = Math.max(val[j], val[i] + 1);
         }
     }
}

动态规划三种解决方案：

递归容易爆，我为人人思路有点不符合现实逻辑，不宜想；人人为我有点像是递归的形式，也有优化的可能，比较好。